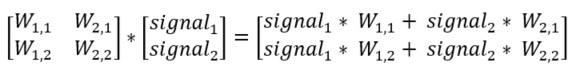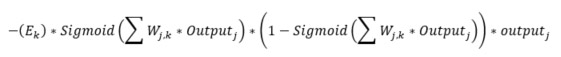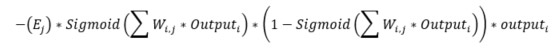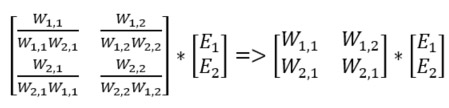Välkommen till del 2 i bloggserien om maskininlärning med neurala nätverk i C#! I det förra inlägget gick jag igenom teorin som behövs för att skriva ett neuralt nätverk från grunden. Om du känner dig bekväm med teorin eller bara vill kolla på kod så är det bara att läsa vidare, annars rekommenderar jag att ni läser del 1 innan ni går vidare med detta inlägg.
TL;DR
Bara utefter kod? Hela källkoden finns på GitHub.
Vi hoppar på implementationen direkt, låt oss börja med att definiera ett skal för nätverket för att ha något konkret att jobba med. Skapa en klass som heter NeuralNetwork som har två metoder; Train och Query. Dessa två metoder är vad man kan förvänta sig av ett enkelt nätverk – Query är till för att fråga efter ett svar och Train är till för att träna upp nätverket så att resultatet från Query skall bli så bra som möjligt. Parametern till Query är tämligen intuitiv medans parametrarna till Train även innehåller ”targets”. Targets är de värden vi vill att nätverket skall svara givet inskickade insignaler – target är alltså vårat facit. Nedan följer koden för skalet.
public class NeuralNetwork
{
public void Train(double[] inputs, double[] targets)
{
}
public double[] Query(double[] inputs)
{
}
}
Vi har lärt oss att ett nätverk består av 3 (eller fler) lager av neuroner – ett ingångs, ett dolt och ett resultatslager. Neuronerna är ihopkopplade med varandra med signaler där varje signal har en vikt. Dessa vikter behöver få ett grundvärde när nätverket skapas. Kom ihåg att vikterna måste vara tillräckligt små för att Sigmoidfunktionen skall fungera korrekt, i detta fall fungerar slumpmässiga tal mellan -0.5 och 0.5.
Lägg till en konstruktor för klassen, en som kräver antalet noder i varje lager samt en inlärningsfaktor. Inlärningsfaktorn är en parameter som kommer påverka funktionen som justerar vikterna, experimentera med denna parameter för att ändra hur snabbt/ långsamt nätverket skall lära sig – till exempel kan det vara användbart att minska inlärningsfaktorn om nätverket har en tendens att ”skjuta över”.
private readonly double _learningRate;
private Matrix _weightHiddenOutput;
private Matrix _weightInputHidden;
public NeuralNetwork(int numberOfInputNodes, int numberOfHiddenNodes, int numberOfOutputNodes, double learningRate)
{
_learningRate = learningRate;
_weightInputHidden = Matrix.Create(numberOfHiddenNodes, numberOfInputNodes);
_weightHiddenOutput = Matrix.Create(numberOfOutputNodes, numberOfHiddenNodes);
RandomizeWeights();
}
private void RandomizeWeights()
{
var rnd = new Random();
//distribute -0.5 to 0.5.
_weightHiddenOutput.Initialize(() => rnd.NextDouble() - 0.5);
_weightInputHidden.Initialize(() => rnd.NextDouble() - 0.5);
}
Konstruktorn har två huvudansvar – skapa två matriser samt sätta dess vikter, slumpmässigt, mellan -0.5 och 0.5. Vad har matriser med detta att göra? Matriser hjälper oss väldigt mycket genom att hålla beräkningarna i nätverket enkla och överskådliga. Detta, plus att matrisberäkningarna inte har någon begränsning vad gäller antal neuroner, gör lösningen generell och liten. Lägg märke till att klassen ”Matrix” inte är en inbyggd typ i C# utan vi måste bygga våran egna. Hela matrisimplementationen finns på GitHub.
Matriser förenklar beräkningarna
Tänk er att skriva alla instruktioner som behövs för att beräkna alla vikter och signaler i ett nätverk som består av tusentals, om inte mer, neuroner – det är nästan omöjligt. Här nedan kommer jag visa varför matriser fungerar så bra i detta scenario.
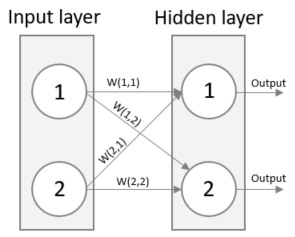
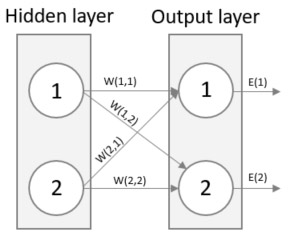
Kommer du ihåg att resultatet från en neuron är den viktade summan av alla inkommande signaler? Se nedan vad som händer om vi beskriver vikterna mellan ingångs och det dolda lagret i den vänstra matrisen och signalerna i den högra och sedan multiplicerar dessa två matriser. Resultatet är en matris som innehåller den viktade summan av alla inkommande signaler. Precis vad vi vill ha! I detta förenklade exempel består nätverket av endast två neuroner i varje lager men det bästa av allt är att denna metod fungerar för valfritt antal neuroner!
En bild säger mer än tusen ord sägs det. Låt oss se om det är sant. Nedan är en bild för att visualisera ovanstående ekvation. Ser du att resultatet från neuron 1 i det dolda lagret är (W(1,1) * Signal 1) + (W(2,1) * Signal 2)? Precis vad som står i den första cellen i matrisen ovan!
Implementationen av Query
Vår kunskap om matriser kommer definitivt hjälpa oss i implementationen av Query. Att jag börjar med Query är för att den är aningens enklare än Train som måste implementera viktjusteringsfunktionerna. I övrigt är Query och Train snarlika. Innan vi tittar på kod så passar det bra att summera vad Query behöver göra.
- Beräkna signalerna till varje neuron i det dolda lagret från ingångsignalerna och dess vikter
- Applicera Sigmoidfunktionen för varje dold neuron
- Beräkna nätverkets resultatsignaler från resultatet av det dolda lagret och dess vikter
- Applicera Sigmoidfunktionen på varje resultatneuron
public double[] Query(double[] inputs)
{
var inputSignals = ConvertToMatrix(inputs);
var hiddenOutputs = Sigmoid(_weightInputHidden * inputSignals);
var finalOutputs = Sigmoid(_weightHiddenOutput * hiddenOutputs);
return finalOutputs.Value.SelectMany(x => x.Select(y => y)).ToArray();
}
Inte alls så mycket kod, eller hur? Metoden börjar med att ta in en array av insignaler som omvandlas till sin matrisrepresentation. Sedan producerar vi resultatet från det dolda lagret genom att applicera aktiveringsfunktionen ”Sigmoid” över varenda viktade insignal till det dolda lagret. Detta resultat beräknas med matrismultiplikation mellan insignalerna och dess vikter, precis som beskrivet tidigare.
Efter detta för vi exakt samma sak igen, skillnaden är att vi använder resultatet från föregående operation som insignal samt vikterna mellan det dolda lagret och resultatlagret. Detta producerar nätverkets resultat. Slutligen returnerar vi resultatet i arrayform. Resultatet är alltid en N*1 matris och kan därför representeras som en vanlig array.
Implementationen av Train
Train är snarlik Query men måste också uppdatera vikterna vid varje anrop. Vi går direkt in på den första, snarlika, delen av implementationen.
public void Train(double[] inputs, double[] targets)
{
var inputSignals = ConvertToMatrix(inputs);
var targetSignals = ConvertToMatrix(targets);
var hiddenOutputs = Sigmoid(_weightInputHidden * inputSignals);
var finalOutputs = Sigmoid(_weightHiddenOutput * hiddenOutputs);
var outputErrors = targetSignals - finalOutputs;
//TODO: Calculate new weights
}
Som sagt, väldigt likt Query. Den enda skillnaden än så länge är att vi också beräknar feldifferensen genom en matrissubtraktion mellan önskat resultat och det faktiska resultatet. Eftersom matrissubtraktion utförs element för element passar den bra till formeln för att beräkna feldifferensen (som är önskat resultat – faktiskt resultat).
Det som saknas nu är viktjusteringsfunktionen. Denna funktion är den sista pusselbiten till ett självlärande nätverk. Från del 1 minns vi att formeln för att justera vikterna mellan det dolda lagret (j) och resultatlagret (k) är:
Vi vet också att en inlärningsfaktor skickas in som parameter i konstruktorn. Inlärningsfaktorn är en faktor som appliceras på ovanstående uttryck. Koden för att justera vikterna mellan det dolda lagret och resultatlagret, d.v.s. egenskapen ”_weightHiddenOutput”, blir då:
_weightHiddenOutput += _learningRate * outputErrors * finalOutputs * (1.0 - finalOutputs) * hiddenOutputs.Transpose();
Ovanstående kod skall alltså stämma överens med formeln – låt oss kontrollera!
- _learningRate är som sagt bara en faktor och inte en del av formeln egentligen
- outputErrors är E(k) som är (önskat värde – faktiskt värde)
- finalOutputs är den första Sigmoid-delen som är över summan av alla signaler till resultatlagret, se linje 5 i Train-metoden
- 1.0 – finalOutputs är den andra Sigmoid-delen
- hiddenOutputs är output(j) delen. Här transponeras ”hiddenOutput” för att möjliggöra matrismultiplikation
Det är värt att nämna att allt detta är matrisoperationer, visst blir det lätt, smidigt och läsbart?
Det enda som saknas nu är viktuppdateringarna mellan ingångslagret och det dolda lagret. Formeln för detta är nästintill identisk med föregående formel, se nedan:
Skillnaden är att ni här använder ingångslagret och det dolda lagret istället för det dolda lagret och resultatlagret (i = ingångslagret, j = dolda lagret). Det finns faktiskt en skillnad till, de felen i det dolda lagret E(j). E(k) var enkelt att beräkna genom att ta differensen mellan önskat och faktiskt värde, E(j) däremot måste beräknas på ett annat sätt. Om ni har läst mitt tidigare inlägg så vet ni att ni kan dela upp felet genom att inspektera hur stor del av felet som respektive neuron bidrog till. I exemplet nedan kan denna uppdelning skrivas som W(1,1) / W(1,1) + W(2,1) och W(1,2) / W(1, 2) + W(2,2). Detta kallas för ”back propagation”.
Om ni multiplicerar varje kvot med felen från resultatlagret så finner ni felen i det dolda lagret. Detta kan göras via en matrisoperation. Ni kan också göra en förenkling av ovanstående formel – ta bort den normaliserande kvoten. Eftersom felet som propagerar tillbaka är proportionellt mot sin vikt, oavsett normaliserande kvoten, kan vi helt enkelt ta bort den. Jämför nedanstående matrismultiplikation före (till vänster) och efter (till höger) förenklingen. Den högra är klart enklare och ger tillräckligt bra resultat.
Matrisen med vikter här ovan är faktiskt transponatet av viktmatrisen mellan det dolda lagret och resultatlagret. Koden för att uppdatera vikterna mellan ingångslagret och det dolda lagret är:
var hiddenErrors = _weightHiddenOutput.Transpose() * outputErrors; _weightInputHidden += _learningRate * hiddenErrors * hiddenOutputs * (1.0 - hiddenOutputs) * inputSignals.Transpose();
Nästan klart
Sådär! Train-metoden är fullständig och vi skall nu ha ett fungerande neuralt nätverk! Du kan behöva dra ner koden för Matrix-klassen samt implementera Sigmoid-funktionen innan koden bygger. Sigmoid-funktionen är liten och enkel – koden visas här nedan. Matrix-klassen finner du på GitHub.
private Matrix Sigmoid(Matrix matrix)
{
var newMatrix = Matrix.Create(matrix.Value.Length, matrix.Value[0].Length);
for (var x = 0; x < matrix.Value.Length; x++)
{
for (var y = 0; y < matrix.Value[x].Length; y++)
{
newMatrix.Value[x][y] = 1 / (1 + Math.Pow(Math.E, -matrix.Value[x][y]));
}
}
return newMatrix;
}
Testkör det neurala nätverket
Dags att testköra nätverket. Det första problemet som vi skall försöka lösa är att känna igen handskrivna siffror. Det finns ett berömt dataset av sådana handskrivna siffror som består av 60 000 träningsposter och ett test-set av 10 000 poster. Ni kan ladda ned er egna kopia av träningsdelen här och testdelen här.
Om ni lägger filerna i C:\Temp så kommer koden på GitHub fungera direkt, annars får ni modifiera sökvägarna i HandwrittenDigits.cs.
Anledningen till att det är två filer, en träningsfil och en testfil, är att ni generellt inte vill använda samma data när man frågar nätverket som man använde för att träna nätverket. Detta skulle med all sannolikhet producera väldigt bra resultat men inte alls fungera lika bra på okänd data. Det sistnämnda är precis vad vi vill göra – producera bra resultat på okänd data, träningsfasen är endast till så att nätverket skall lära sig känna igen mönster som kan appliceras på nytt data.
För att köra nätverket med minst data-settet så kör ni konsolapplikationen med följande Main-funktion:
static void Main(string[] args)
{
Problems.HandwrittenDigits.Run();
Console.ReadLine();
}
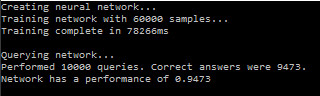
Det är att föredra att köra applikationen i releaseläge (eller i debug fast utan debugging) – prestandan påverkas kraftigt negativt när debugging är på. Låt oss se hur nätverket presterar när vi kör applikationen.
Inte så pjåkigt! Nätverket lyckades svara rätt 94,73% av fallen, med andra ord 9473 gånger av de 10000 testfallen. Reflektera över det, efter att nätverket tränats, av helt andra dataposter, kunde nätverket svara på vilken handskriven siffra en person skrev med en prestanda på ungefär 95%. Här nedan följer en bild på vilka typer av siffror som vi matar in i nätverket.
Iris data set
Ett annat berömt dataset är Iris – som du hittar här. Det består av 150 poster som i sin tur har 4 parametrar och ett svar. Parametrarna är dimensionerna på kronblad och löv, svaret är en art av Iris. Mer information om datasettet finner man på Wikipedia. Eftersom detta dataset är väldigt mycket mindre kan man förvänta sig ett mer utspritt resultat eftersom nätverket får färre poster att träna med.
Kör applikationen med följande Main-funktion:
static void Main(string[] args)
{
Problems.Iris.Run();
Console.ReadLine();
}
Detta ger en prestanda, i snitt, på 96%. Nätverket kunde alltså bestämma typen av Iris i 96% av fallen. Det som händer i praktiken är att nätverket lär sig hur varje parameter korrelerar med det önskade värdet (svaret) och vikterna uppdateras kontinuerligt för att minska felet i resultatlagret. Programmet ovan blandar datasettet slumpmässigt och väljer sedan ut 100 av dem som träningsdata och resterande 50 blir då testdatat.
XOR
Nätverket kan också tränas till att lösa XOR-funktionen. Denna funktion tar två parametrar, a och b, och returnerar falskt om både a och b är falska eller sanna, annars returneras sant. Nätverket tränas med dessa två parametrar och träningsproceduren repeteras 2000 gånger (detta kallas för 2000 epochs). Efter detta frågar vi nätverket 4 gånger, en per kombination av a och b.
Som ni ser är det inga problem att lösa funktionen. Ni kan själv köra detta genom följande Main-funktion:
static void Main(string[] args)
{
Problems.XOR.Run();
Console.ReadLine();
}
Som ni ser kan nätverket tränas till att lösa många olika problem – problem som nätverket inte har någon tidigare kunskap om. Det är faktiskt lite magiskt, tycker jag. Ni får gärna använda denna implementation, eller vidareutveckla den, hur ni vill. Koden finns i sin helhet på GitHub. Om ni vill labba med olika dataset kan jag rekommendera detta arkiv.
Har ni frågor eller vill veta mer? Tveka inte att kontakta mig, Andreas Hagsten!
Andreas Hagsten
Software Developer, Infozone