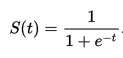Maskininlärning med ett neuralt nätverk i C# – Del 1 – Teorin

Jag har alltid varit fascinerad av Artificiell Intelligens, att skriva mjukvara som kan lösa ett problem utan att behöva berätta för den exakt hur problemet skall lösas. Att skriva mjukvara som faktiskt lär sig hur ett problem skall lösas – med lite hjälp på traven.

I denna serie av blogginlägg kommer jag gå igenom hur vi faktiskt kan skriva vårt egna neurala nätverk i C#. Till en början tänkte jag hoppa rakt in i kodandet och förklara alla begrepp allt eftersom, men det visade sig relativt omgående bli för mycket på en gång. Därför blev det en bloggserie av detta. Den första delen kommer beröra teorin bakom ett artificiellt neuralt nätverk medans del nummer två kommer handla om implementationen och när vi kommit till del tre är det hög tid för reflektion kring och samt optimisering av nätverket. Målet med det neurala nätverket är att det skall kunna lösa ett antal problem och jag kommer demonstrera hur vi tränar nätverket att lösa XOR-funktionen, sinus-funktionen samt att känna igen handskrivna siffror.

Innan vi börjar så vill jag bara klargöra att jag inte är en expert på området, snarare motsatsen – en nybörjare. Denna bloggserie kan därför innehålla fel, både inom den matematiska och neurala nätverks-teorin. Jag har skaffat mig denna kunskap genom att först läsa en jättebra bok, ”Make your own neural network”, för att sedan fördjupa mig online. Innehållet kan därför vara influerat av boken.

Vad är ett neuralt nätverk?

Jag kommer inte gå in i detalj i vad ett neuralt nätverk är då det finns mycket bra material att läsa på andra ställen. Men kortfattat så är ett neuralt nätverk ett nätverk av neuroner där varje neuron mottager och avger signaler från andra neuroner. Varje signal är tilldelad en vikt och en neuron avger en utsignal om och endast om summan av alla insignaler överstiger ett visst tröskelvärde, detta betyder att en neuron inte nödvändigtvis avger en utsignal givet en insignal. En insignal kan alltså ignoreras om den inte är stark nog. Man kan relatera till oss själva där kroppen kanske inte reagerar mot hetta förens det är fara för att man bränner sig – först då får kroppen en signal om att dra undan handen från plattan. Vi kommer snart få se hur man kan modellera ett sådant nätverk bara genom att använda gymnasiematte.

Konceptet runt artificiellt neuralt nätverk

Att skriva och eller förstå ett neuralt nätverk kan verka överväldigande och man kan lätt tro att det kräver mattematik på forskningsnivå. Jag trodde det. Ack så fel jag hade, man kan faktiskt skriva ett enklare neuralt nätverk bara genom enkel matematik så som relativt enkel algebra och matrismanipulationer. Låt oss gå igenom den teori som krävs för att gå vidare till implementationen som följer i del 2.

Lager av neuroner

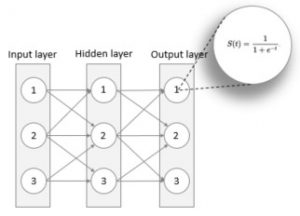
Ett neuralt nätverk består oftast av 3 lager – ingångslagret, resultatlagret samt ett dolt lager. Det dolda lagret ligger mellan ingångs- och resultatlagret och antalet kan variera från noll till många – normalt är det endast ett lager. Ingångslagret består av lika antal neuroner som det finns inparametrar. Om du t.ex. har ett dataset med 10 parametrar kommer det då sannolikt finnas 10 neuroner i ingånglagret. Resultatlagret kommer ha lika många neuroner som det finns svar. Ett exempel är ett Booleskt svar som då kan anta värdena sant eller falskt, i detta fall kommer nätverkets resultatlager ha en neuron då en neuron har ett decimalt värde som då kan tolkas som sant eller falskt (t.ex. 0.01 kan tolkas som falskt, 0.99 som sant). Antalet neuroner i det dolda lagret är inte lika skrivet i sten, här får man experimentera sig fram, men en tumregel är ett värde som ligger mellan antalet i ingånglagret och antal i resultatlagret.

En neurons aktiveringsfunktion

Som nämnt ovan, ”en neuron avger en utsignal om och endast om summan av alla insignaler överstiger ett visst tröskelvärde”. Varje neuron har en så kallad aktiveringsfunktion som är ansvarig för att trycka ner eller skicka vidare en utsignal givet en insignal. Det finns ett antal aktiveringsfunktioner som används i dessa nätverk och vi kommer använda en av de vanligaste – Sigmoid. Sigmoid-funktionen har en S-formad kurva med värden mellan 0 och 1. Denna funktion kommer anropas för varje neuron när en insignal inkommer. Sigmoids definition och form kan ses här nedan.

Sigmoids funktion

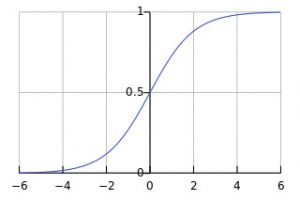
Som ni märker går funktionen mot 0 när X går mot minus oändligheten och mot 1 när X går mot oändligheten. Man kan också se att resultatet från funktionen faktiskt är väldigt nära 0 redan vid X = -4 och väldigt nära 1 när X = 4, detta betyder att man måste hålla insignalerna små och att utsignalerna kommer ligga mellan 0 och 1. Detta betyder att man i normalfallet måste normalisera insignalerna och de-normalisera utsignalerna.

Ett neuralt nätverk med tre lager där varje neuron
är associaserad med en Sigmoidfunktion

Viktning av signaler

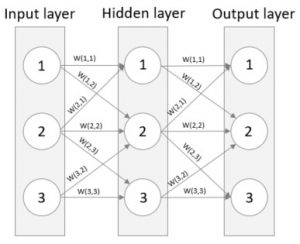
Den mest centrala delen av ett neuralt nätverk är vikterna som appliceras på varje signal – nätverket är tränat och har lärt sig att lösa problemet om och endast om vikterna är satta så att nätverket producerar rätt resultat. Bilden nedan illustrerar signalernas vikt.

Signalernas vikter

Normalt sett generarar man initiala vikter slumpmässigt mellan 0 och 1 eller -1 och 1. Kom ihåg att Sigmoidfunktionen är som mest användbar för låga X-värden, d.v.s. låga insignaler. Om man istället skulle ha stora vikter skulle man riskera att mätta nätverket genom att generera konstanta av/på-signaler. Bara för att slå ner spiken i kistan – om man har en vikt på 1000 så skulle insignalen till Sigmoidfunktionen alltid vara stor och utsignalen skulle då alltid vara 1. Konstanta ”på- eller av-signaler” är att mätta ett nätverk vilket medför att påverkad neuron inte kan lära sig.

Det är dags att ge ett exempel på hur man kan beräkna en neurons utsignal. Om vi låter O(X) vara utsignalen från neuron X och låter N(1,2) vara den första neuronen i det andra (d.v.s. dolda) lagret så får man för den första neuronen i det andra lagret O(N(1,2)) = Sigmoid(O(N(1,1)) * W(1,1) + O(N(2,1)) * W(2,1)). Om vi använder samma formel för det dolda lagrets andra neuron får vi O(N(2,2)) = Sigmoid(O(N(1,1)) * W(1,2) + O(N(2,1)) * W(2,2) + O(N(3,1)) * W(3,2)). De olika delarna är färgkodade för att göra det lite mer läsbart. För att summera, utsignalen för en given neuron är lika med Sigmoid av summan av alla viktade insignaler. Detta görs för alla neuroner i det neurala nätverket!

Feldifferens i utsignalen

Vi har precis gått igenom formeln för hur man beräknar utsignalen genom att vikta insignalerna och sen använda aktiveringsfunktionen på resultatet. Om man skulle testköra nätverket, genom att mata in insignaler och sedan låta dessa signaler färdas genom nätverket för att procudera ett resultat, så skulle man med all sannolikhet inte vara nöjd med resultatet. Vi skulle ha en differens mellan vårat resultat och vårat önskade värde. Ett neuralt nätverk behöver lära sig ett problem för att det skall ha en chans att lösa problemet, att bara skicka in insignaler i ett otränat nätverk och tro att vi magiskt ska få ut rätt svar är lite naivt. Vårat mål är att hitta de vikter så att feldifferensen blir så låg som möjligt, när detta är uppnått så är nätverket tränat.

Man kan ta det Booleska exemplet, d.v.s. ett resultat som är antingen sant eller falskt. Nätverket kommer då ha en neuron i resultatlagret och denna neuron kan ha ett resultat mellan 0.01 och 0.99 (avrundat till två decimaler), kom ihåg att Sigmoid avger värden mellan 0 och 1. Om vårat önskade värde är 0.99 (sant) och det faktiska resultatet är 0.3 så kan vi beräkna feldifferensen genom (önskat resultat – faktiskt resultat) som är 0.69. Drömdifferensen är 0. Målet nu är att hitta de vikter som gör att nätverket avger en så låg feldifferens som möjligt, en metod för att göra just det är ”Back propagating”.

Back propagating

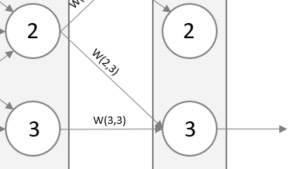
När man propagerar bakåt börjar man från resultatlagret och arbetar sig genom nätverket tillbaka till ingångslagret samtidigt som vikterna uppdateras. Man inser snabbt att en neurons feldifferens är orsakad av insignaler från flera andra neuroner från föregående lager. Se bilden nedan där utsignalens feldifferens är orsakad av W(2,3) och W(3,3), därför måste man uppdatera både W(2,3) och W(3,3) för att minska feldifferensen. Detta görs genom att dela upp feldifferensen proportionerligt enligt deras vikt eftersom de trots allt bidragit till felet i storleksordning av deras vikt. Så, om W(2,3) är dubbelt så stor som W(3,3) delar vi upp felet så att W(2,3) får dubbelt så mycket.

En enkel formel kan hittas för denna fördelning av felet – W(2,3) / W(2,3) + W(3,3). Denna formel är sann för varenda lager i nätverket när vi propagerar bakåt. Feldifferensen i resultatlagret är tämligen uppenbart (önskat värde – faktiskt värde), däremot är feldifferensen för neuroner i det dolda lagret inte like uppenbart. Lyckligtvis kan man, som skrivet, applicera ovanstående formel på det dolda lagret också. För att beräkna feldifferensen för en neuron i det dolda lagret tar man summan av de fel som härstammar från neuronen där felet för en signal beräknas enligt föregående formel.

Gradient descent

Vi har sett hur man får fram hur mycket varje insignal bidrar till feldifferensen, men vi har inte gått igenom hur man faktiskt uppdaterar vikterna. Hur finner man en ny vikt som faktiskt minskar denna feldifferens i resultatlagret? Man skulle kunna tänka sig en ”brute force” variant där man väljer nya vikter slumpmässigt för att sedan inspektera resultatet, denna gissningslek kan visa sig bära frukt för väldigt små nätverk men kommer snabbt bli väldigt dyra sett till beräkningskraft eftersom normala nätverk, med hundratals neuroner per lager, med lätthet har miljoner av kombinationer av vikter.

Finns det ett bättre sätt att uppdatera vikterna så att feldifferensen minskas? Det finns lyckligtvis en välkänd matematisk metod för detta, en metod som gradvis rör sig mot den lägsta punkten – Gradient descent. Det finns sannolikt en annan funktion som faktiskt kan räkna ut alla vikter direkt, men en sådan funktion är alldeles för komplex. Gradient descent passar väldigt bra i de fall man arbetar med för komplexa funktioner då den kan ge oss en approximation genom att gradvis gå mot en lägre och lägre feldifferens givet en vikt.

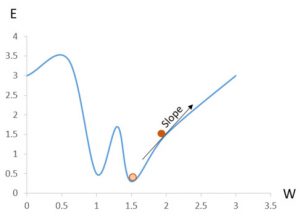
Med andra ord, om man tänker sig ett vanligt koordinatsystem där feldifferensen E ligger på Y-axeln och vikten W på X-axeln, då kommer Gradient descent att röra sig mot det lägsta felet E givet en vikt W. Se bilden nedan, anta att den mörkorangea cirkeln är det nuvarande felet och att målet är den ljusorangea cirkeln. Det Gradient descent kan göra är att hjälpa en finna i vilken riktning man behöver röra sig för att finna det lägsta E, i detta fall den motsatta riktningen – man behöver alltså minska vikten! Man kan också se en möjlig fallgrop i bilden, om man minskar vikten för mycket, t.ex. till 1.25, så kommer man att röra sig mot det lokala minimat vid W = 1 vilket inte är det sanna minimat som är vid X = 1.5. Man måste alltså ändra vikten med ett tillräckligt litet tal för att förhindra att man skjuter över men tillräckligt stort för att bibehålla en bra prestanda.

Man kan tycka att det är lätt att finna det minsta felet E, och absolut, det kan man. Dock är det så att man i neurala nätverk inte bara beror av en variabel, som i bilden ovan, utan hundratals. Faktum är att vi i nästa del kommer demonstrera närverket genom att träna det för igenkänning av handskrivna siffror. Insignalerna till nätverket kommer då vara bilder med 28*28 pixlar där varje pixel motsvarar en neuron – nätverket beror alltså av 784 parametrar. Det är en väldigt komplex funktion att skriva för att beräkna ut rätt vikter.

Man behöver alltså hitta den riktning som gör att man kan uppdatera vikterna för att minska feldifferensen, man behöver beräkna derviatan dy/dx, eller i detta fall dE/dW. Funktionen för att finna feldifferensen är som bekant (önskat värde – faktiskt värde) men vi behöver mjuka till den lite, därför kvadrerar vi den. Att kvadrera har andra fördelar också, det gör att gradienten blir kvadratiskt liten för små fel vilket för att man förhindrar en ”överskjutning” som kan medföra att man hittar ett lokalt minima istället för det sanna. Så, den slutgiltiga feldifferensfunktionen blir (önskat värde – faktiskt värde)².

Eftersom felet beror på utsignalen och utsignalen beror på vikterna (felet ökar/minskar beroende på utsignalens värde och utsignalens värde ändras om vikten ändras) kan man formulera om dE/dW till dE/dO • dO/dW. Den första termen har vi redan gått igenom, vilket är (önskat – faktiskt)² – låt oss skriva det som (target – output)² från och med nu. Derivatan av (target – output)² är 2*(target – output). Den andra termen är mer komplex och vi kommer inte gå in i detalj där. Vi vet att Sigmoid-funktionen appliceras på utsignalen från en neuron, så den andra temen blir derivatan av Sigmoid vilket redan är definierad av andra och är Sigmoid(x) * (1 – Sigmoid(x)) där x är den viktade summan från alla inkommande signaler. Sätter vi ihop bägge delarna får vi ett slutgiltigt uttryck för att beräkna justeringen av vikterna, detta uttryck är:

-(target – output) * sigmoid(∑weight*output)*(1-sigmoid(∑weight*output)) * hidden layer output. Konstanten 2 har försvunnit då man endast är intresserad av riktningen, uttrycket är också negerat för att man vill gå mot lägre vikter då riktningen är positiv och högre vikter då riktningen är negativ.

Detta uttryck kommer användas i nästa del i bloggserien då vi kommer implementera det neurala nätverket i C#.

Sammanfattning

Det här var en hel del teori! Låt oss summera det vi gått igenom i punktform

• Ett ingångslager, noll till många dolda lager samt ett resultatlager
• Lika många neuroner i ingångslagret som det finns inparametrar
• Lika många neuroner i resultatlagret som det finns svar
• Antalet neuroner i det dolda lagret är inte fördefinierat men tumregeln är att det skall vara någonstans mellan antalet i ingångs- och resultatlagret
• Varje neuron har en aktiveringsfunktion, i denna bloggserie används Sigmoid
• Signalernas vikt är centrala. Varje länk mellan neuroner har en vikt associerad med sig
• Målet är att uppdatera vikterna så att nätverket avger nästintill korrekta utsignaler
• Back propagation används för att uppdatera vikterna baserat på hur mycket de bidragit till feldifferensen
• Använd Gradient descent för att hitta den vikt som ger det lägsta felet

I nästa inlägg kommer vi ta all denna teori och applicera det på ett neuralt nätverk byggt från grunden i C#!

Har ni frågor eller vill veta mer? Tveka inte att kontakta mig, Andreas Hagsten!

Andreas Hagsten
Software Developer, Infozone

*Bildreferens: Wikipedia