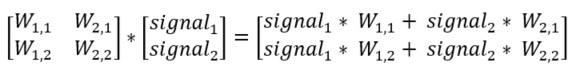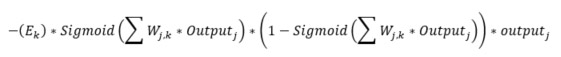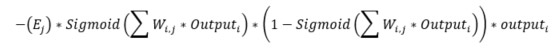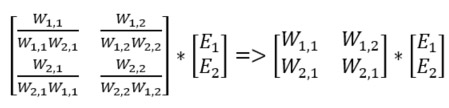This is the second part of three in a blog series about Machine learning using a Neural Network. In the previous post, I went through the theory needed to write a shiny neural network, from scratch, in C#. If you feel comfortable with the theory or just want some code then keep on reading, otherwise I recommend reading part 1 before reading any further.
TL;DR
Source code can be found here.
Let us start by defining a shell for our network, just to have something to work with. I’ve defined a class named NeuralNetwork that has two methods; Train and Query. These methods are the two core methods you will see in such networks. Query is understandable – one needs to ask the network for some result given some input. Train, on the other hand is less intuitive, if a network should be able to solve a problem it needs to be trained. In the training scenario, one needs to pass in the input and target values. The target values are those we want the network to emit when it’s queried for the given input values.
public class NeuralNetwork
{
public void Train(double[] inputs, double[] targets)
{
}
public double[] Query(double[] inputs)
{
}
}
There it is, the first step towards a neural network.
We have learned that a network is built using an input, an output and a hidden layer of neurons. The neurons are connected to each other with signals with an associated weight. These weights need to be initialized when the network is created. Remember that the weights need to be small for the Sigmoid activation function to work properly, in this case a random distribution between -0.5 and 0.5 will suffice.
Let’s add a constructor in our class, one that requires the number of nodes in each layer as well as a learning rate. The learning rate is a parameter that acts as a factor on the weight adjustment function, tweak this one to either increase or decrease the weights learning rate – it can prove useful to lower this if the network keeps overshooting, for instance.
private readonly double _learningRate;
private Matrix _weightHiddenOutput;
private Matrix _weightInputHidden;
public NeuralNetwork(int numberOfInputNodes, int numberOfHiddenNodes, int numberOfOutputNodes, double learningRate)
{
_learningRate = learningRate;
_weightInputHidden = Matrix.Create(numberOfHiddenNodes, numberOfInputNodes);
_weightHiddenOutput = Matrix.Create(numberOfOutputNodes, numberOfHiddenNodes);
RandomizeWeights();
}
private void RandomizeWeights()
{
var rnd = new Random();
//distribute -0.5 to 0.5.
_weightHiddenOutput.Initialize(() => rnd.NextDouble() - 0.5);
_weightInputHidden.Initialize(() => rnd.NextDouble() - 0.5);
}
The constructor does two things in particular – create two matrices and initializes the with random weights between -0.5 and 0.5. Wait, matrices? Yes! Matrices helps to keep the instructions needed to calculate a neural network small and neat. Note that the Matrix class is written from scratch and is therefore not a part of C# or .NET. The full implementation is found @ GitHub.
The use of matrices
Imagine writing all the instructions needed to calculate the weights and signals through a network of thousands (or more) neurons – it will be close to impossible. I’ll show just why matrices works so well in our scenario.
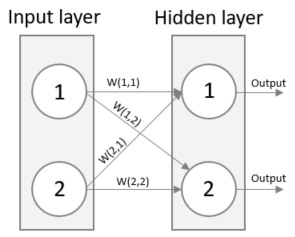
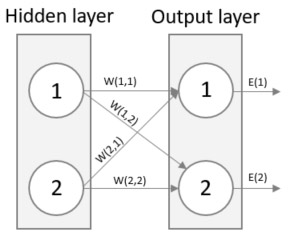
Remember that the output of a neuron is the weighted sum of all incoming signals? Have a look below what happens if we put all weights between the input and hidden layer in the left-side matrix and the signal itself in right-side matrix and then multiply them. The resulting matrix is the weighted sum of all incoming signals. In this simple example, the network only consists of two neurons in each layer, but the best part is that this method works for any number of neurons which will make the solution generic and flexible.
An image can usually clarify any doubts, look below for an image representation of the above equation. See how the output of neuron 1 of the Hidden layer is (W(1,1) * Signal 1) + (W(2,1) * Signal 2)? Just as the above matrix.
Implementation of Query
Our knowledge of how helpful matrices are will aid the implementation of the Query-method. The reason that I begin with Query over Train is that Query is less complicated as it does not need to update any weights. Remember that the network is trained, and ready to be queried, when the weights are set correctly. Before we dig into some code, lets summarize what we need to do here.
- Calculate the signals to each neuron in the hidden layer using the networks inputs and their associated weights
- Apply the Sigmoid activation function on each hidden neuron
- Calculate the networks output signals using the output from the hidden layer and their associated weights
- Apply the Sigmoid activation function on each output neuron
public double[] Query(double[] inputs)
{
var inputSignals = ConvertToMatrix(inputs);
var hiddenOutputs = Sigmoid(_weightInputHidden * inputSignals);
var finalOutputs = Sigmoid(_weightHiddenOutput * hiddenOutputs);
return finalOutputs.Value.SelectMany(x => x.Select(y => y)).ToArray();
}
Not too much code, right? Let’s walk through each line. First we accept an array of inputs that gets converted to its matrix representation. Then we produce the output from the hidden layer by applying the Sigmoid activation function over each input to the hidden layer. That input is calculated using matrix multiplication between the signals from the input layer and their weights, just as described earlier.
Next, we do the exact same thing again, but using the result from the previous operation as input and using the weights between the hidden and output layer instead. This produces the actual network result. Transform it to an array of doubles (the result is always a N*1 matrix and can be represented using an regular array) and return it. We are done with the query method!
Implementation of Train
This implementation is very similar to Query but it also need to update the weights at the end of each round. Let’s have a look at the first part of the implementation.
public void Train(double[] inputs, double[] targets)
{
var inputSignals = ConvertToMatrix(inputs);
var targetSignals = ConvertToMatrix(targets);
var hiddenOutputs = Sigmoid(_weightInputHidden * inputSignals);
var finalOutputs = Sigmoid(_weightHiddenOutput * hiddenOutputs);
var outputErrors = targetSignals - finalOutputs;
//TODO: Calculate new weights
}
As said, very much alike Query. The final outputs are calculated using matrix multiplication with Sigmoid around that. The output errors have also been calculated using matrix subtraction. Matrix subtraction is element-wise subtraction and is therefore conforming with our formula for calculating the output error (target – actual).
Now, the weights need to be adjusted for the network to train itself. From the previous post, we saw that the weight adjusting function for weights between the hidden (j) and the output (k) layer is:
We have also taken note of a “learning rate” being passed in to the constructor. The learning rate is a factor applied to the above expression. Let’s see the code that adjust the matrix “_weightHiddenOutput”:
_weightHiddenOutput += _learningRate * outputErrors * finalOutputs * (1.0 - finalOutputs) * hiddenOutputs.Transpose();
The above code should correspond to the formula – let’s see!
- _learningRate, as said, is only the factor and not a part of the expression per say
- outputErrors is E(k) which is (target – actual)
- finalOutputs is the first Sigmoid-part which is over the sum of all the signals to the result layer, as can be seen on line 5 in the Train-method
- 1.0 – finalOutputs is the second Sigmoid-part
- hiddenOutputs is the output(j) part. The hiddenOutputs is transposed to make it possible to perform matrix multiplication.
It is worth mentioning that all the operations are performed on matrices. You can see how small and concise the code becomes.
To complete the Train method, we need to update the weights between the input and the hidden layer. The function needed is indeed almost identical to the above, have a look:
The function is identical, just shifted to the input/hidden layer instead of hidden/output (i = input, j = hidden). But wait, one parameter needs to be calculated, the hidden errors. In the previous post we seen how to split the errors between nodes that contributed to it as W(1,1) / W(1,1) + W(2,1) and W(1,2) / W(1, 2) + W(2,2) for the example below. This is called back propagation.
If we multiply each fraction with the errors, we will find the errors of the hidden layer. We can do this using matrices. What we also can do, to simplify the expression is to remove the normalizing fraction, since the larger the weight the more of the error will be carried back and that is exactly what we want. See that the right-hand expression is simpler than the left hand but will still do what we want.
The resulting left hand side matrix is the transpose of the weight matrix of the hidden output. The code is as follows:
var hiddenErrors = _weightHiddenOutput.Transpose() * outputErrors; _weightInputHidden += _learningRate * hiddenErrors * hiddenOutputs * (1.0 - hiddenOutputs) * inputSignals.Transpose();
Almost done
Thats it! The Train method is complete and we have a working Neural network…almost. Since C# does not have any built-in Matrix type we need to build one from scratch, in addition the Sigmoid function needs to be implemented. The Sigmoid function can be seen here below:
private Matrix Sigmoid(Matrix matrix)
{
var newMatrix = Matrix.Create(matrix.Value.Length, matrix.Value[0].Length);
for (var x = 0; x < matrix.Value.Length; x++)
{
for (var y = 0; y < matrix.Value[x].Length; y++)
{
newMatrix.Value[x][y] = 1 / (1 + Math.Pow(Math.E, -matrix.Value[x][y]));
}
}
return newMatrix;
}
You can find the code for Matrix along with the full Neural Network over at GitHub.
Running the Neural Network
Time to see what the network can do! The first problem that it will tackle is recognizing handwritten digits. There is a famous data set for this, it consists of a training set of 60 000 records and a test set of 10 000. You can download your own copy of the training set here and the test set here.
If you download the files to C:\Temp, the code sample on GitHub will work out of the box, otherwise you’ll need to modify the paths in HandwrittenDigits.cs source file.
The reason why there are two files, a training and a test data set, is that we generally do not want to use the same data we used during training when querying the network. It would most likely produce very good results to query on the training data but we would not know how the network would perform on other data. The very essence of a neural network is that it should perform well on unknown data, the training phase merely teaches the network to recognize patterns to be applied to fresh data.
To run the network on the mnist data set, run the console application with the following Main function:
static void Main(string[] args)
{
Problems.HandwrittenDigits.Run();
Console.ReadLine();
}
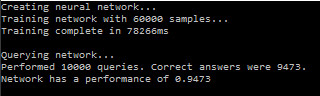
It is preferable to run the application in release mode (or in debug mode without debugging) – the performance hit running in debug is huge. Let’s see how the network performs when running the application.
That is not too bad of a result! The network came up with the correct digit 94.73% of the times, i.e. in 9473 of the 10000 test samples. Reflect on that. After the network was trained, it could determine which digit a person had written with an accuracy, or performance, of 94%. Just to proof that the network receives images as input, here are a few samples of digits getting passed into the network:
Iris data set
Another famous data set is the Iris data set found here. It consists of 150 records which in turn consists of 4 parameters and a result. The parameters are sepal and petal dimensions and the output is an Iris species. More information about the data set can be found at Wikipedia. Since this data set is smaller we can expect a more diverse result as we run the sample repeatedly, remember that the network is seeded with random weights.
Running the application using the main function:
static void Main(string[] args)
{
Problems.Iris.Run();
Console.ReadLine();
}
Gives the performance (on average) 96%, i.e. it could determine the correct type of Iris in 96% of the cases. What happens here (and for all other cases) is that the network learns how each parameter correlates to the target value and the weights gets updated accordingly to reduce the error in the output. The program shuffles the data set and then selects 100 of them for training and the remaining 50 is used for testing.
XOR
The network can also be trained to solve the common XOR-function. The function takes two parameters, a and b, and returns false if both a and b are false or true, otherwise true. The network is trained using the two input parameters and the training is repeated 2000 times (this is called 2000 epochs). When querying the network, it outputs the following response:
As you can see, there are no problem at all solving the function. You can run this application by using the following main function:
static void Main(string[] args)
{
Problems.XOR.Run();
Console.ReadLine();
}
As you can see, the network can be trained to solve various problems – problems that is has no prior knowledge to. Amazing, if you ask me! You are more than welcome use this implementation yourself, just download it from GitHub. If you want to try other data sets I can recommend this archive.
Do you have any questions, see any errors or just want to get in contact? Do not hesitate to contact me, Andreas Hagsten
Andreas Hagsten
Software Developer, Infozone